いろいろな数列の和 552621

「等比数列の和」 等比数列の和における公式の成り立ち、等比数列における和のいろいろな問題をとりあげます。 第 5 回 「∑（シグマ）の利用」 ∑の性質、∑の公式から、各数列の和を∑を利用して解答する問題をとりあげます。 第 6 回Try IT（トライイット）のいろいろな数列の和の問題の様々な問題を解説した映像授業一覧ページです。 いろいろな数列の和の問題を探している人や問題の解き方がわからない人は、単元を選んで問題と解説の映像授業をご覧ください。 ピックアップ映像授業 例題 特殊な分数の和（3） 高校数学B 練習 特殊な分数の和（3） 高校数学B2 2節 いろいろな数列 21 数列の和とΣ記号;

Excel エクセルで等差数列の和を計算する方法

いろいろな数列の和

いろいろな数列の和-いろいろな数列の和 等差数列の和 、 等比数列の和 Σk 、 Σk 2 、 Σk 3 奇数列の和 、 遇数列の和 初項が1で、各項の係数が等差数列、文字部分が等比数列である数列の和 その他代表的な数列の和 丶 jin 丶7 いろいろな数列(1) (わざわざ，因数分解をもう一度学習するのではなく，この数列を学習しながら，因数分解をするような気持ちで行きましょう)。

Xdfrac12 Abc 2 b C Lihat Cara Penyelesaian Di Qanda

新数学B 1章「数列」 4 次の数列の初項から第項までの和を求めなさい。 12，23，34，45，⋯ この数列の第 𝑘 項は 𝑘 𝑘1 ;の 等比数列 (2) 第7 項が5，第 項が－21 である等差数列{a n}について，次の問いに答えよ。 ① 初項a，公差d を求めよ。 ② 初項から第何項までの和が最大となるか。また，その最大値を求めよ。 (3) 等比数列{b n}について， 1 1 b ＋ 2 1 b ＝ 3 2 ， 3 1 b 4 1 b ＝ 27いろいろな数列の和 これまで、等差数列や等比数列など様々な数列の和を計算してきました。 ここでは、それら以外の特殊な数列の和を計算します。 ここでは問題を通して計算方法を解説していきます。 次の和を計算せよ。 を利用します。 すると

7 章：数列 1：いろいろな数列 1 いろいろな数列 11 等差数列 299 (1) s ò2 ¬ ) 1 p K s ) » w H10 ò x p K { h \ w » w H10 ò T H ò p w è x p K { ¢ b Ô » À G £ (2) s ò T H10 ò p w è U100 p s ò T H ò p w è U350 p K O s s ) 等差数列 例： 2 4 6 ⋯ 100 = 2550 246\cdots 100=2550 2 4 6 ⋯ 100 = 2550 初項が a a a ，末項が l l l ，項数が n n n であるような等差数列の和は， 1 2 n (a l) \dfrac{1}{2}n(al) 2 1 n (a l) →等差数列の和の公式の例題と証明など 等比数列 例： 1 2 4 8 16 = 31 =31 1 2 4 8 16 = 313 3節 漸化式と数学的帰納法 31 漸化式;

33いろいろな数列 36 トピックス 拡張 例題322 いろいろな数列の和 練習322 例題323 分数の数列の和1 いろいろな数列の和 基本公式 1 ^ a k d ` a a d ¦ a d ^ a n d ` n ^ a n d ` n k 2 1 2 1 1 2 1 1 （等差数列の和） 2 > 1@ 1と表されるから，求める和は 𝑘 𝑘1 ;

S シグマ の計算 数学ｂ いろいろな数列の和 Youtube

Xdfrac12 Abc 2 b C Lihat Cara Penyelesaian Di Qanda

数学bのいろいろな数列の和やシグマ計算の学校では習えない解き方 uhei 年3月25日 / 年3月27日 入試に出ている数列の和の問題。いろいろな数列の和（93 ページ） 一般項が等差数列と等比数列の積で表される数 列の和を求める計算について，等比数列の和を 求める計算との関連を取り上げた。 標準的な内容は本文で一通り扱っている。 3 点が一直線上にあることの証明（35 ページ）数列・順列・組み合わせ計算機 「数列・順列・組み合わせ計算機」はいろいろな数列、順列、組み合わせの計算を行う計算機です。 普通の電卓としての機能はありません。 簡単に等差数列の和などを計算することができます。 わざわざ公式に値を入れ

等比数列の和 N 1

高校生 数学b 東京書籍 01 1章1節数列 いろいろな数列 教科書解答解説 赤城 ᐡᐤᐡ

数列・順列・組み合わせ計算機 「数列・順列・組み合わせ計算機」はいろいろな数列、順列、組み合わせの計算を行う計算機です。 普通の電卓としての機能はありません。 簡単に等差数列の和などを計算することができます。 わざわざ公式に値を入れ いろいろな等比数列の和 等比数列の和の公式： a ( 1 − r n) 1 − r \dfrac {a (1r^n)} {1r} 1−ra(1−rn) をいろいろな等比数列に使ってみましょう。 公比が負の数でも分数でもOK。 2 2 ( − 1 3) 2 ( − 1 3) 2 ⋯ 2 ( − 1 3) 9 22 (\dfrac {1} {3})2 (\dfrac {1} {3})^2\cdots 2 (\dfrac {1} {3})^9 22(−311数列5時間 2等差数列とその和3時間 3等比数列とその和3時間（本時はその第2時） 4和の記号Σ 5階差数列 6いろいろな数列の和 7漸化式と数列 8数学的帰納法 評価規準等は，https//wwwniergojp/kaihatsu/hyouka/ kou/04_kou_suugakupdf を参考にすること

3講 等差数列の和 1節 等差数列と等比数列 問題集 3章 数列

1

 1 1節 数列とその和 11 数列; 等差数列の和の公式でやってもイマイチわからないので、わかりやすくお願いいたします。 数学 いろいろな数列の和 この問題の矢印の部分にはどうやったらなるんですか？香川亮の数学基本大全 数列 数学b15a いろいろな数列の和(5) 差を作る 数列

いろいろな数列の和 N 2のとき と定義する問題としない問題があります 数学 教えて Goo

等差数列の和

 実は、この式には、等比数列の和がいくつも隠れているのです。 私たちが求めることができる等比数列の和は \ a ar ar^2 \cdots ar^{n1} ar^{n} \ という形。 そこで、いま邪魔になるのは、\( 2 ar \)の\( 2 \)のような、前についている自然数。いろいろな数列の和 これらの問題の解き方を教えてください 数学bのいろいろな数列の和やシグマ計算の学校では習えない 数列 シグマ（Σ）の使い方や表し方と注意点;等比数列の和 初項 a から、公比 r の等比数列の初項から第 n 項までの和を Sn とすると その他の数列 例：1，2，1，2，1，2，1，・・・・・ の一般項は an ＝ ｛ 3＋（－1） n ｝ ／ 2 いろいろな数列の和

分数の数列の和 高校数学ｂ Youtube

高校数学無料問題集 数ｂ 第１章 数列 いろいろな数列の和 桝 ます Note

1 等差数列、等比数列、いろいろな数列の和が求めることができる。 2 数列の極限値を求めることができる。であるから，数列{ sin nπ}はすべての項が0 の数列である。 よって，この数列は 収束し，極限値は0 ④ tan 𝜋 4 =1，tan 3 4 𝜋=−1，tan 5 4 𝜋=1，⋯⋯ であるから，数列{tan 2𝑛−1 4 𝜋}は−1と1が交互に現れる数列である。よって，𝑛を限りなく 数列の基本7｜ 等差×等比型の数列の和は引き算がポイント 等差数列 3, 5, 7, 9, 等比数列 2, 6, 18, 54, を考えます． このような 等差×等比型の数列の初項から第 n 項までの和は， n を使って表すことができます．

高校数学b 等差数列の和s Nの最大 最小 受験の月

高校生 数学b 東京書籍 01 1章1節数列 いろいろな数列 教科書解答解説 赤城 ᐡᐤᐡ

いろいろな数列の和･数b 高校数学に関する質問 勉強質問2節 いろいろな数列 1 数列の和と記号 ∑ 問1 例2 問2 例3 問3 和の記号 ∑ 例1 自然数の累乗の和香川亮の数学基本大全 数列 数学b16a いろいろな数列の和(6) シグマ公式の証明 数列 数学B16A いろいろな数列の和(6) シグマ公式の証明 香川 亮 ログイン

2

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

例題3 数列 1, 13, 135, 1357, について (1) 第 n 項 1357 (2n1) を n の式で表せ。 (2) 初項から第 n 項までの和を求めよ。 練習問題3 数列 1 2 1･22 2, 2 2 2･33 2, 3 2 3･44 2, について，初項から第 n 項までの和を求めよ。 そもそもどんな和を考えるのだったかというと ∑ k = 1 n k 2 = 1 2 2 2 3 2 n 2 でした。 考えることは『二乗の和が出てくるような上手い形の式がないか』です。 ここで見るべきなのは次の恒等式です。 ( k 1) 3 − k 3 = 3 k 2 3 k 1 これは Focus もしある関数 f ( x) が f ( k) が m 次式であるとすると、 f ( k 1) から f ( k) を引くと残る式は m − 1 次式である という等比数列の和の成 り立ちを，記号や数 式，四則演算の組み 合わせを用いて的 確に表現している。 7 ・等比数列の和の公 式を適切に利用し て，等比数列の和 を求める。 ・等比数列の和に関 する条件が与えら れたとき，初項や 公比を求める。 や，効率よく処理す

第1章 数列 Edupa Info Pdf Math Hm Hmb 1 17 Pdf数列の和と一般項 B 数列和 第n部分和 の列の階差 数列 の初項から第 項までの和を とする

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

いろいろな数列の和の問題を見る ＞ すべての授業の「要点まとめノート」「問題・解答」をPDF無料ダウンロードできる 学校で使っている教科書にあわせて勉強できる6 4 Þ @ 5 l Í𝑘 6 6 4 Þ @ 5 e Í𝑘 6 4 Þ @ 5 l 1 6 h21 h41 1 2 h h21 l28705 いろいろな数列 51 和の記号 ∑ 例えば，数列{an}と自然数n が与えられたとき，「数列{an}の初項から第n 項までの和を求めよ」と いう問題を考えよう．例えば，初項から第10 項までの和を a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 と書くことはできるが，第100 項までとなると大変である．このよう

数b色々な数列の和ここまでの展開を教えて欲しいです 1 2 Yahoo 知恵袋

再開 数学おじさん この秋は数列に決めた 数学おじさんのブログ

前回 https//googl/Yjbnpl 次回 https//googl/WR9QRj動画のプリント（19ch） http//www19chtv/サブチャンネル とある男が数列23 等比数列08 一般項 和 数列24 等比数列09 積 逆数 和 数列25 等比数列10 等差数列と等比数列の混合 数列26 等比数列11 等差と等比の混合 数列27 等比数列12 応用 大小 数列28 等比数列13 応用 大小 数列29 等比数列14 複利計算 数列30 いろいろな数列01 Σ 桝塾数学無料問題集「数列」第4講「いろいろな数列の和」京成佐倉 query_builder 練習問題 今回のメインは、「部分分数分解」です（他のも少し入ってま

数列と級数 京極一樹の数学塾

桝塾 数学無料問題集 数列 第４講 いろいろな数列の和 京成佐倉 練習問題 ブログ

和を求めることができ る。 数列の定義や表 記について理解 し，問題解決や証 明に活用すること ができる。 4 単元（題材）の指導計画（全14時間） 内 容 時間数 内 容 時間数 1節 等差数列と等比数列 9時間 2節 いろいろな数列 8時間6 4 Þ @ 5 l Í 𝑘 6𝑘 ;いろいろな数列 a n = (等差数列の項) × (等比数列の項) a n = (等差数列の項) × (等比数列の項)の和

５分間studying 数列 6 等比中項と整数の和 数 Bを ぶっ飛ばせ

48s96ub7b0z5f Net Touhisuuretsu

いろいろな数列の一般項や和を計算できる。 いろいろな数列の一般項や和を部分的に計算できる。 いろいろな数列の一般項や和を計算できない。 評価項目3 無限数列や無限級数の極限および簡単な関数の極限を求められる。

数学b色々な数列の和 この問題の解説お願いいたします Yahoo 知恵袋

数 Bを ぶっ飛ばせ 15年01月

高校数学 数b 動画 いろいろな数列の和 の問題 19ch

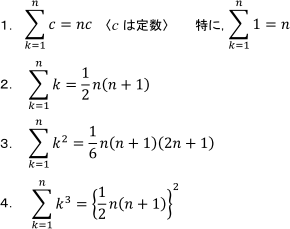
数列 数列の和の公式の使い方 数学b 定期テスト対策サイト

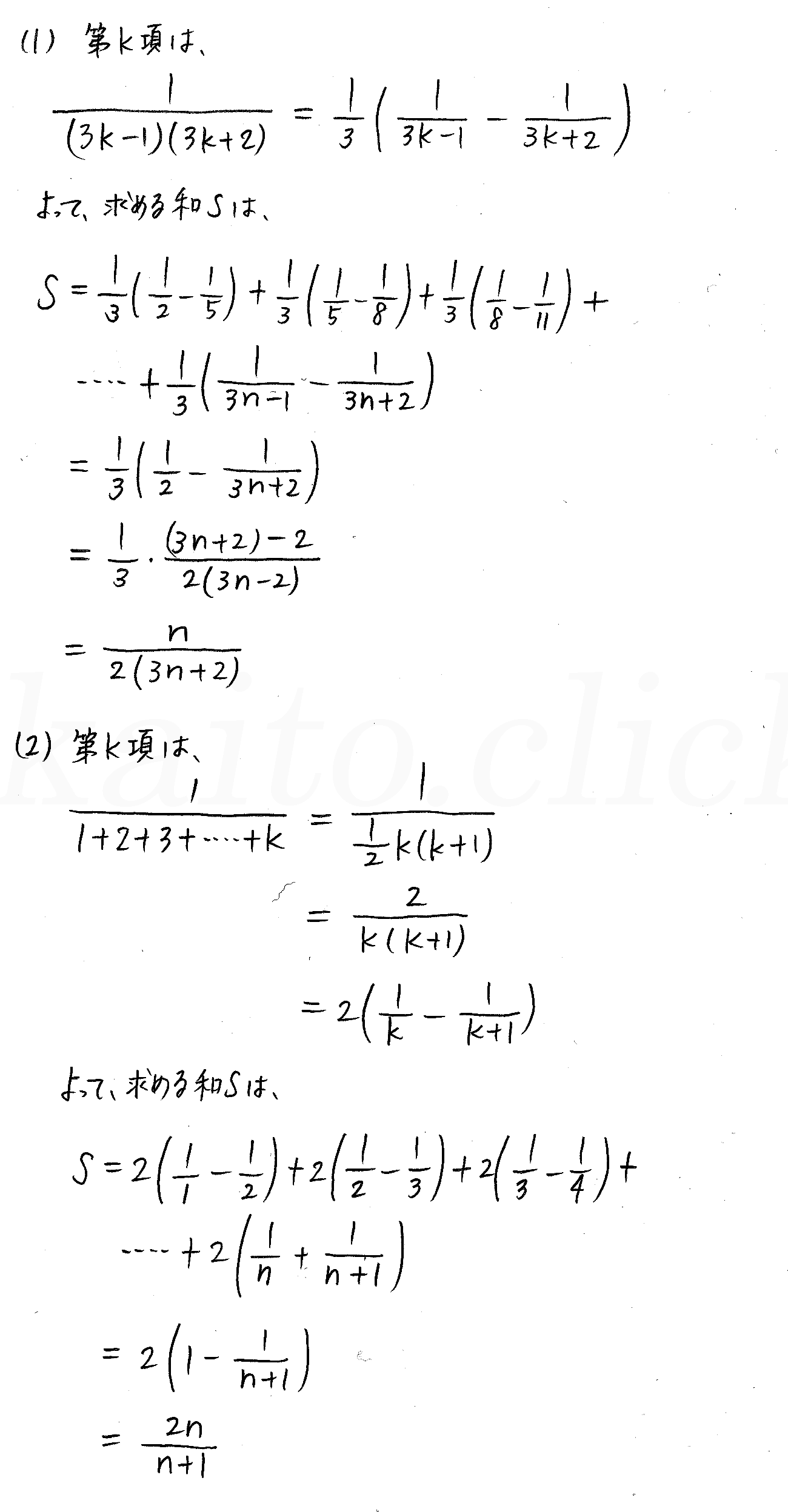
改訂版 クリアー数学b P158 いろいろな数列の和

Xdfrac12 Abc 2 b C Lihat Cara Penyelesaian Di Qanda

高校数学b 和と一般項の関係 映像授業のtry It トライイット

等差数列 等比数列の形の数列の和 高校数学 身勝手な主張

至急でお願いしたいです すみません いろいろな数列の和です Clear

数列の和から一般項を求める 大学受験の王道

Www Mext Go Jp Component A Menu Education Micro Detail Icsfiles Afieldfile 17 05 16 011 Pdf

ゆーあ 今日中に数bのワーク終わらせたいところではある 数列 階差数列しかわかんないから ここらへん全部赤で移せばいいかな 解説読んでも全く理解出来ねえ ベクトル全問正解したら赤点回避できたらしないかなあ

数学bのいろいろな数列の和についてです 2 の問題を教えて Yahoo 知恵袋

高校数学b S と等差 等比数列の和 例題編 映像授業のtry It トライイット

いろいろな数列の和 の勉強法のわからないを5分で解決 映像授業のtry It トライイット

数列の和を求める問題です 途中からよく分からなくなりました Clear

Studydoctor分数の数列の和 高校数学ｂ Studydoctor

数列の応用問題 京極一樹の数学塾

数列 順列 組み合わせ計算機 On The App Store

最も人気のある 1足す1は3 1足す1は3 ネタ

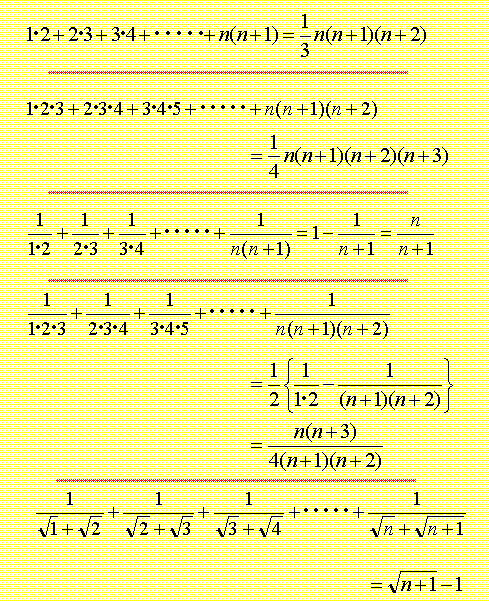
数列 いろいろな数列の和

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

3講 いろいろな数列の和 2節 いろいろな数列 問題集 3章 数列

3講 いろいろな数列の和 2節 いろいろな数列 問題集 3章 数列

高校数学無料問題集 数ｂ 第１章 数列 いろいろな数列の和 桝 ます Note

Www Mext Go Jp Component A Menu Education Micro Detail Icsfiles Afieldfile 17 05 16 012 Pdf

いろいろな数列の和 の勉強法のわからないを5分で解決 映像授業のtry It トライイット

数列の公式はどうして成り立つの N番目の数や和の求め方を本質から理解しよう 中学受験ナビ

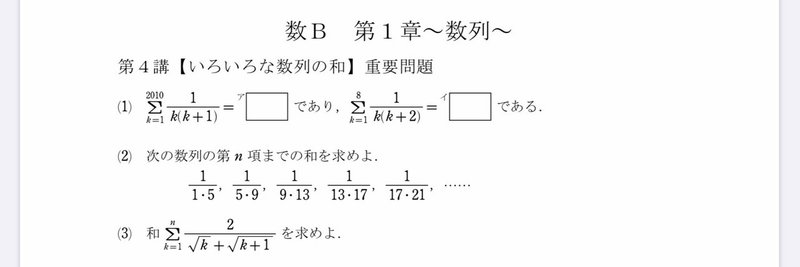
高校数学無料問題集 数ｂ 第１章 数列 いろいろな数列の和 桝 ます Note

等差数列の和の公式の証明を超分かりやすく解説するよ

高2 数学b いろいろな数列の和 高校生 数学のノート Clear

1

等比数列の和について 数学 苦手解決q A 進研ゼミ高校講座

新課程 3trial数学ｂ P153 ８ いろいろな数列の和

Excel エクセルで等差数列の和を計算する方法

赤で囲まれている恒等式を利用して どのようにしたら 下線から 下線に変えられるので Clear

48s96ub7b0z5f Net Tousa Suuretsu

高校数学 数b 動画 いろいろな数列の和 の問題 19ch

数学用語解説 高校 数b

等差 等比型

高校数学無料問題集 数ｂ 第１章 数列 いろいろな数列の和 桝 ます Note

ベスト 9 3 1 3 1 答え シモネタ

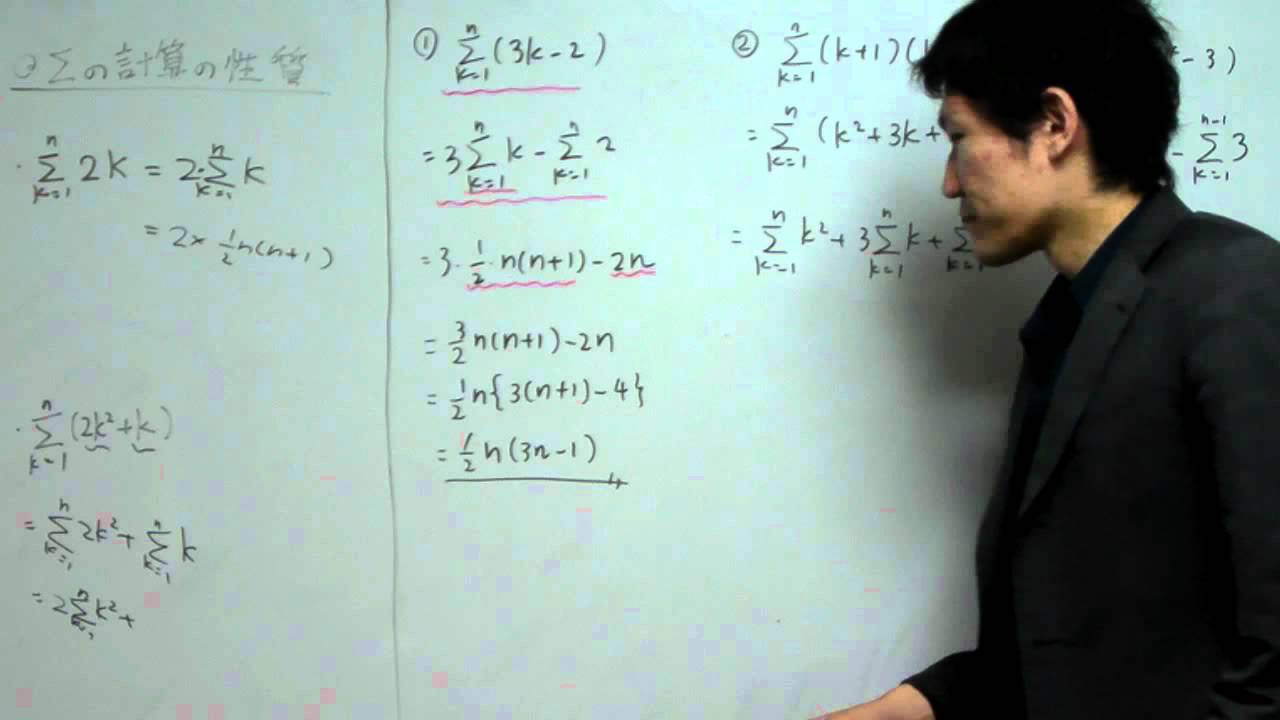
S シグマ の計算 数学ｂ いろいろな数列の和 Youtube

等差 等比 の和 2次式 等比 の和 おいしい数学

高校数学 数b 動画 いろいろな数列の和 の問題 19ch

数列 公式は意味の分かる形で覚えよう 受験生応援し隊 Presented By Forest

いろいろな数列 2

2

数列の基本６ 部分分数分解を用いて計算する数列の和

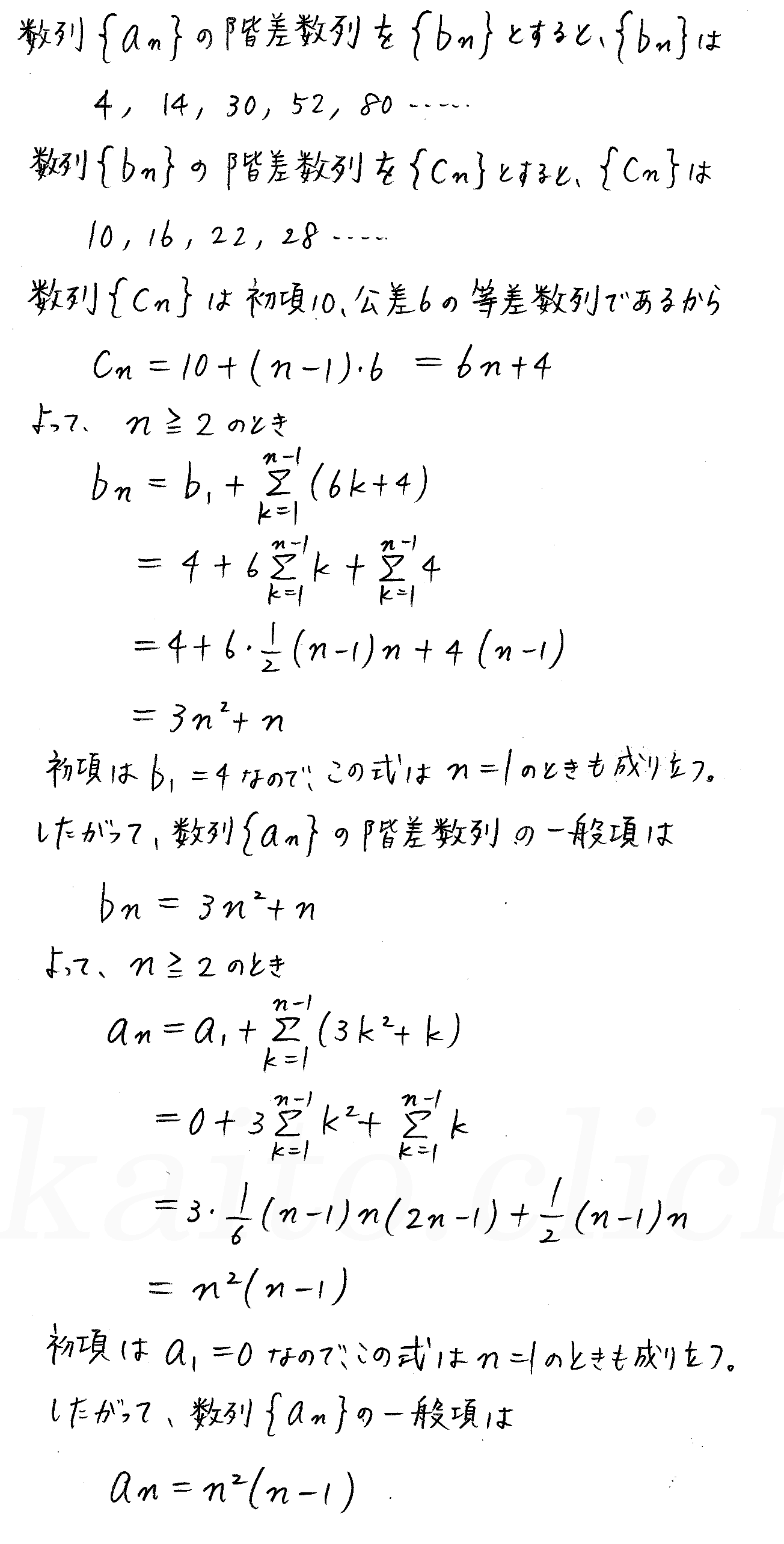
新課程 3trial数学ｂ P154 ８ いろいろな数列の和

数列の和から数列の一般項を求める問題です F1 数学 箱根駅伝ブログ

高校数学b Sの性質と数列の和の公式 S公式 Sk Sk Sk 受験の月

3

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

部分分数分解のやり方のコツ 公式と応用までわかりやすく解説

高校数学数bいろいろな数列の和についての質問です 問 ｓ 1 Yahoo 知恵袋

等差数列の和の最大 符号が変わる場所 大学受験の王道

数列からゼータへ オイラーの手計算 ザギエの数値計算 そして サイエンス テクノロジー 研究 社会連携 京都産業大学

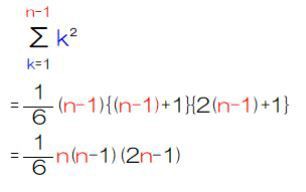
数列 数列の和 S の話 すうがくラボのブログ

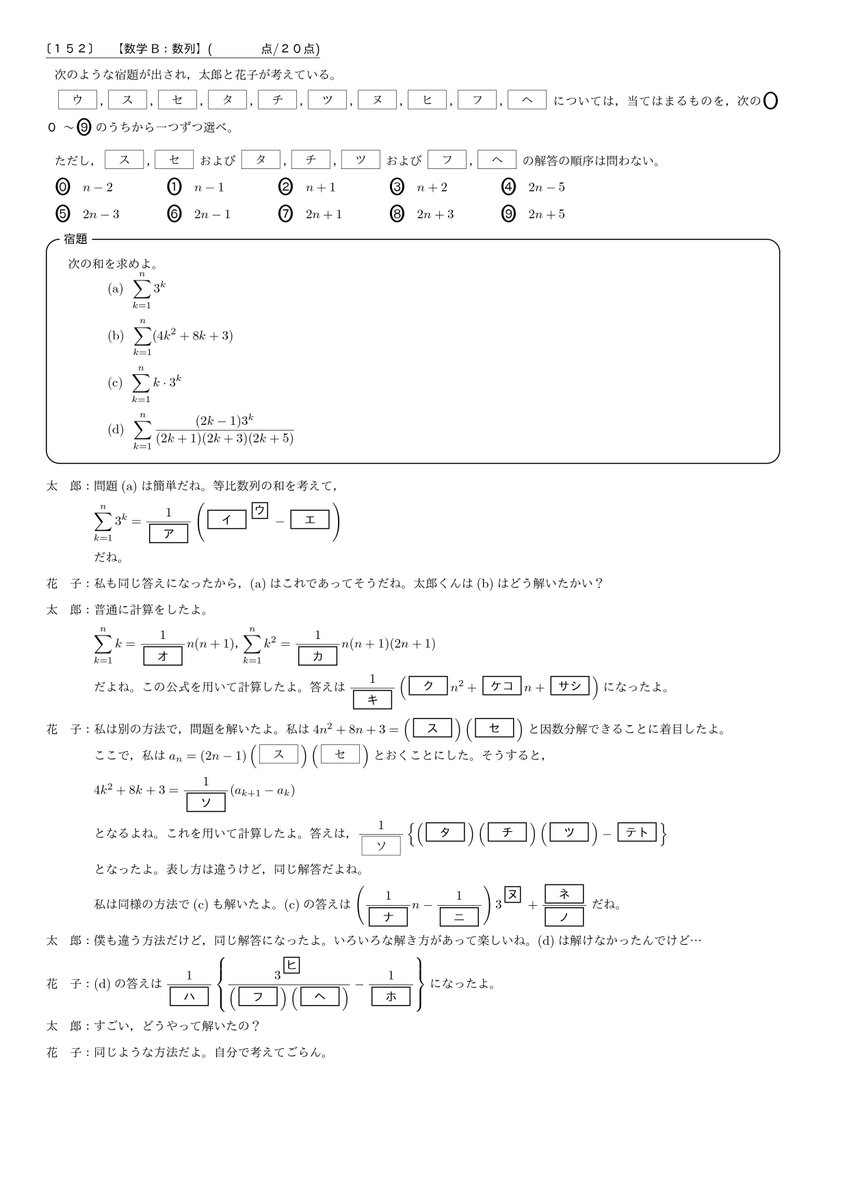
共通テスト 数学 予想問題演習 １５３ 数学ｂ 数列の問題です いろいろな数列の和 を求めよう 共通テストでは 別解 を問う問題が出題されそうです １つの問題に対して 複数の切り口で考えられるようになろう 問題を通じて解法を身につけ それを

階差数列

17数列 Pukiwiki

数列の和で用いる重要な２つの考え方 数学b 数列 そーまのブログ屋さん

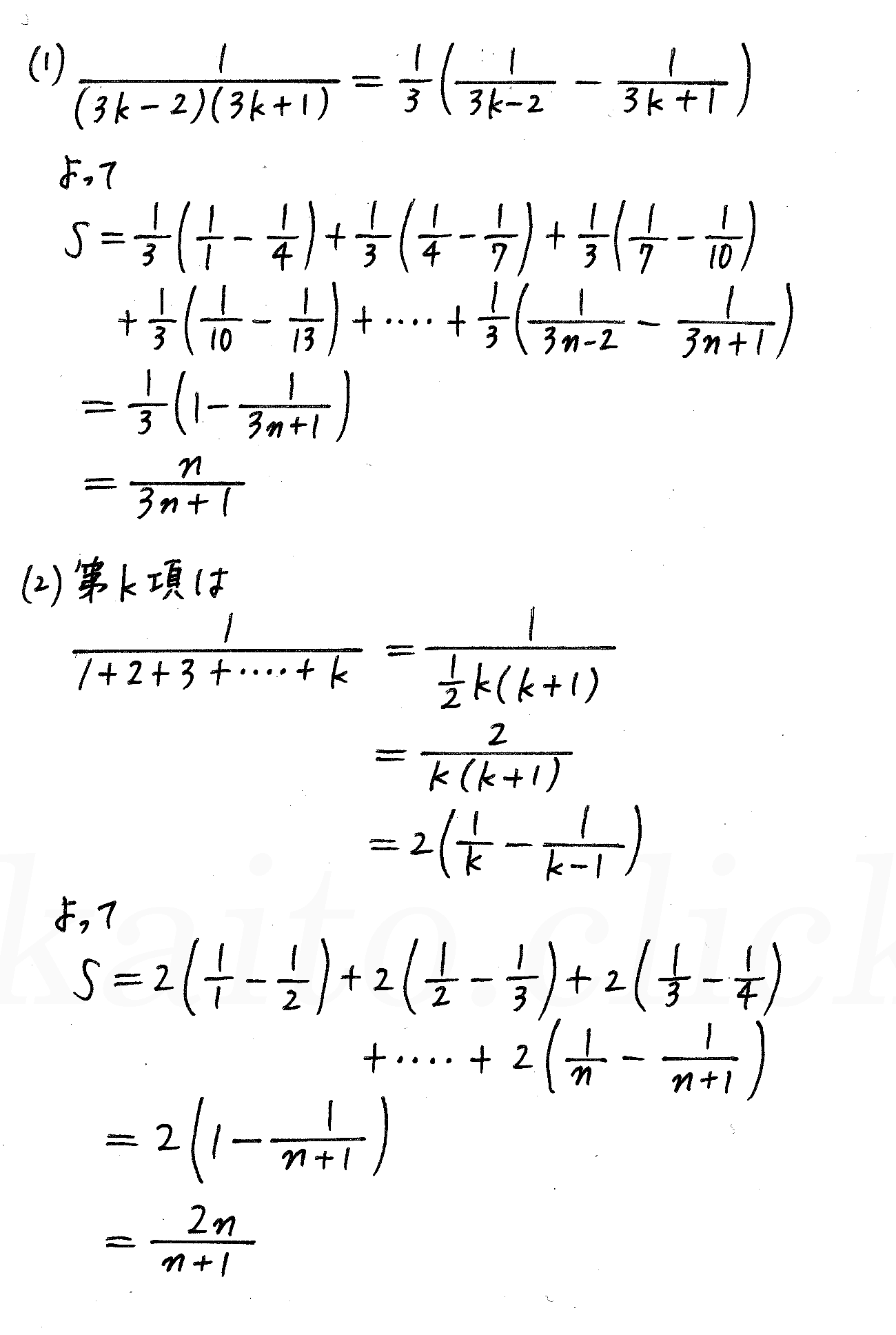
改訂版 3trial数学b P159 ８ いろいろな数列の和

数学ii Bチェック リピート 第7章 1いろいろな数列 8 いろいろな数列の和 Pukiwiki

高校数学 数b ８０ いろいろな数列の和 Youtube

1

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

数列の和の求め方

誤答から学ぼうシリーズ 等差数列 等比数列 型の数列の和 ほのぼの数学頑張ろう

22 4 クァンダ Qanda で解き方を見る

分数の数列の和について 1行目で括る数に文字を入れない方が良いんで 数学 教えて Goo

いろいろな数列の和 富岡市の総合学習塾 トータルアカデミー

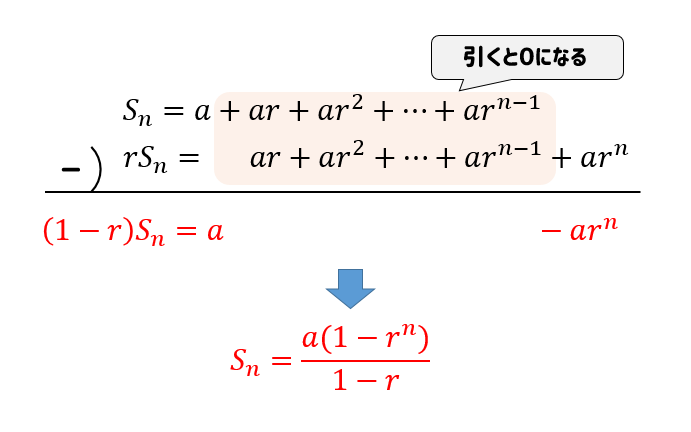
等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

第３講１節 いろいろな数列の和 ３ ｃｏｓの和はｓｉｎ Schoolmath S Diary

第３講１節 いろいろな数列の和 ４ ｓｉｎの和は ｃｏｓ Schoolmath S Diary

いろいろな数列の和 富岡市の総合学習塾 トータルアカデミー

いろいろな数列の和 Jsciencer

48s96ub7b0z5f Net Bunsuunosuuretsunowa

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

数学 B 数列7 色々な数列の和 Youtube

部分分数分解の公式 やり方と分数数列の和の求め方 理系ラボ